
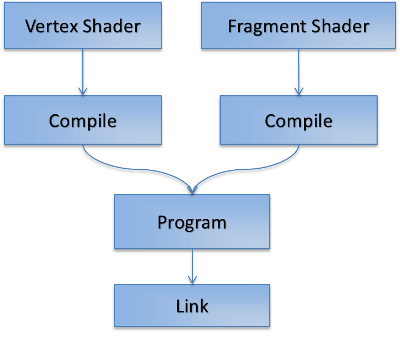
#define PI 3.14 //inputs from vertex shader varying vec2 vTexCoord0 We only store the distance if it's less than what we've already got. For each fragment on the x-axis, we iterate through each pixel of the occluder map on the Y axis, then sample using polar coordinates to determine whether we've hit a shadow-caster.

Thanks to "nego" on the LibGDX forums, I am now using a more efficient solution, which is done entirely in a shader. One is described here, using blending modes. There are a number of ways we could create this shadow map. The more rays, the more precision in our resulting shadows, but the greater the fill-rate. In our case, we have lightSize number of rays, or 256. We take the minimum distance so that we "stop casting the ray" after hitting the first occluder (so to speak). If the ray hits an occluder half way from center, the normalized distance will be 0.5 (and thus the resulting pixel will be gray). So, if one of our red arrows does not hit any occluders, the normalized distance will be 1.0 (and thus the resulting pixel will be white). Each pixel in the resulting 1D shadow map describes the minimum distance to the first occluder for that ray's angle. We normalize the distance of each ray to lightSize, which we defined earlier. The texture on the right represents the "polar transform." The top (black) is the light center, and the bottom (white) is the light edge. On the left, we see each ray being cast from the center (light position) to the first occluder (opaque pixel in our occlusion map). An easy way to visualize it is to imagine a few rays, like in the following: Our x-axis represents the angle theta of a "light ray" from center i.e. The texture is very small (256x1 pixels), and looks like this: Now we need to build a 1D lookup texture, which will be used as our shadow/light map. Step 2: Build a 1D Shadow Map Lookup Texture The resulting "occlusion map" might look like this - with the light at center - if we were to render the alpha channel in black and white: But for now we'll just use the default SpriteBatch shader, and only rely on sampling from the alpha channel. We could use a custom shader here to encode specific data into our occlusion pass (such as normals for diffuse lighting). opaque pixels will be shadow -casters, transparent pixels will not. translate(mx - lightSize / 2f, my - lightSize / 2f) īatch. translate camera so that light is in the centerĬam. set the orthographic camera to the size of our FBOĬam. To do this in LibGDX, we first need to set up a Frame Buffer Object like so: The larger the size, the greater the falloff, but also the more fill-limited our algorithm will become. Our algorithm will expect the light to be at the center of this "occlusion map." We use a square power-of-two size for simplicity's sake this will be the size of our light falloff, as well as the size of our various FBOs. This way, our shader can sample our scene and determine whether an object is a shadow-caster (opaque), or not a shadow-caster (transparent). The first step is to render an "occlusion map" to an FBO. Special thanks to "nego" on LibGDX forums, who suggested some great ideas to reduce the process into fewer passes. As you can see I'm using the same placeholder graphics for the occluders. My technique is inspired by Catalin Zima's dynamic lighting, although the process discussed in this article is rather different and requires far fewer passes.
The idea is an extension of my previous attempts at shader-based shadows, which combines ideas from various sources. The following animation best demonstrates what's happening: The basic steps involved are (1) render occluders to a FBO, (2) build a 1D shadow map, (3) render shadows and sprites. My technique is implemented in LibGDX, although the concepts can be applied to any OpenGL/GLSL framework. Because of the high fill rate and multiple passes involved, this is generally less performant than geometry shadows (which are not per-pixel). Let's do a quick comparison.Detailed here is an approach to 2D pixel-perfect lights/shadows using shaders and the GPU. If you want to use LWJGL, why learn something else first? There really isn't much of a difference between OpenGL in C and with LWJGL anyways. I learned it that way without ever writing a line of C. There is no reason why you can't learn to think in OpenGL by using LWJGL. So essentially, yes, I'm putting the cart before the horse.


 0 kommentar(er)
0 kommentar(er)
